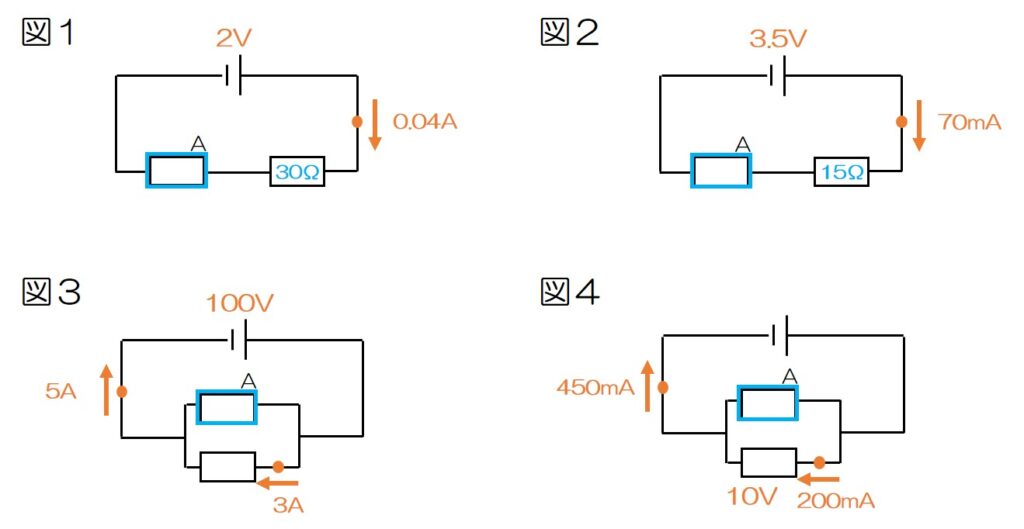
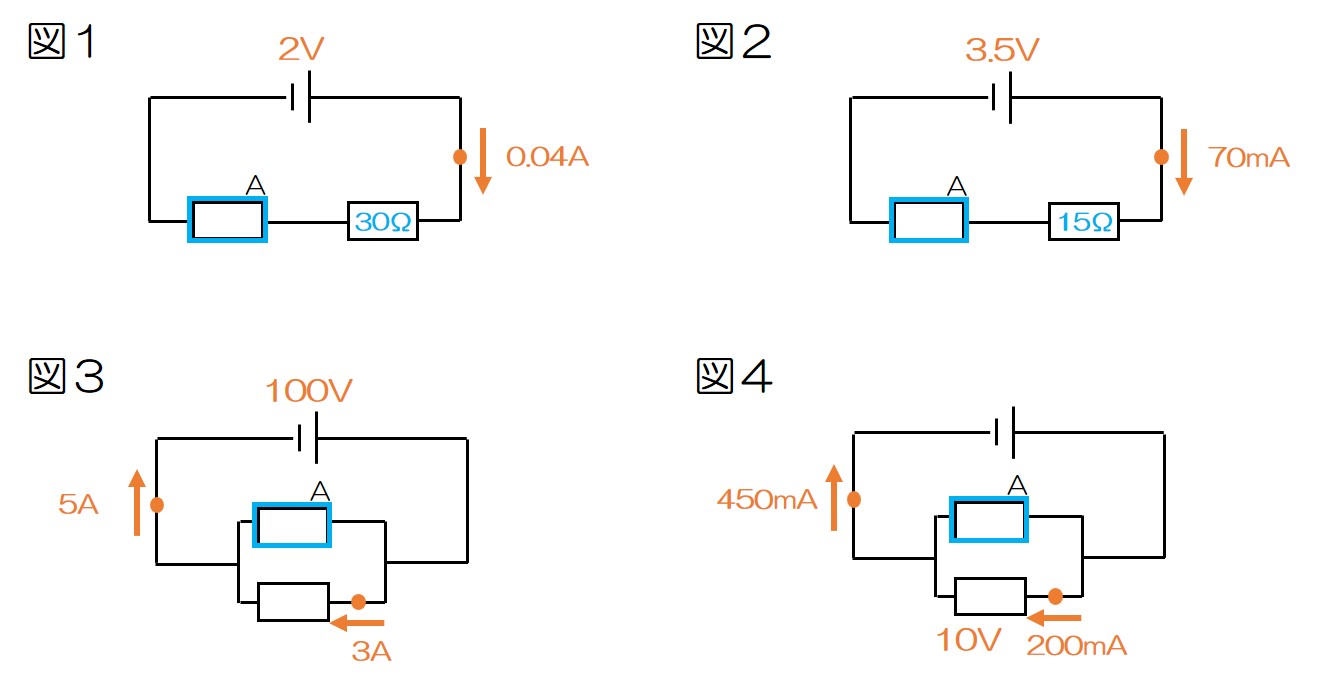
Q.図1~図4の回路において、抵抗器Aの抵抗の大きさを求めなさい。
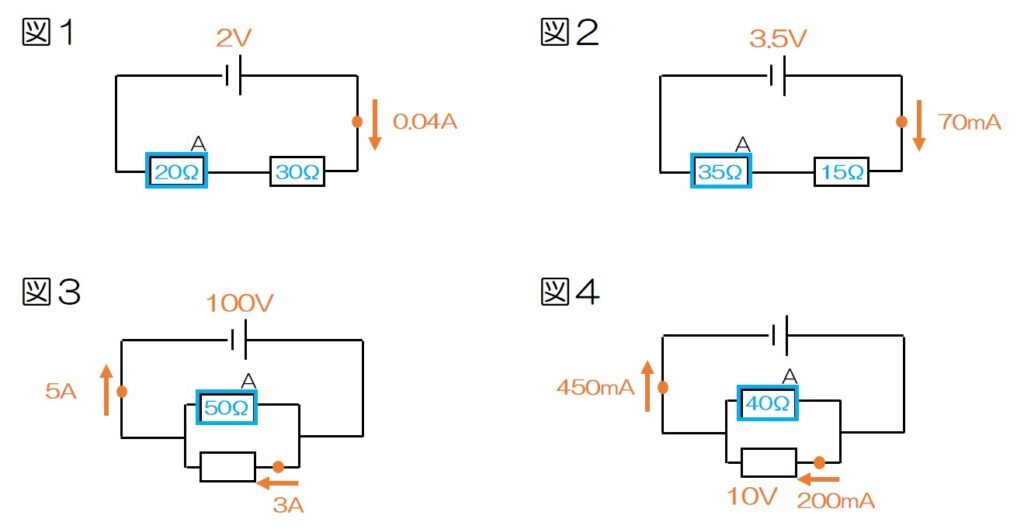
A. 下の図

目指すは「バオ~ムエキスパート」や!今から解説するで!
解説
↑ の記事はもう読んでくれたかな?
「電流」で直列、並列回路に流れる電流について
「電圧」で直列、並列回路に加わる電圧について
「抵抗(電気抵抗)」でバオ~ムの式について説明してるよ!
ここまでくると問題も難しくなってきたね!
でも、基本を1つ1つしっかりおさえていけば恐れることは何もない!
この練習問題を解いてバオ~ムエキスパートになろう!
今回は図1~図4の問題を1問ずつ解説するよ!
それじゃあ、早速見ていこう!
図1の解説
まず注目すべきは「回路全体の電圧」と「回路全体の電流」!
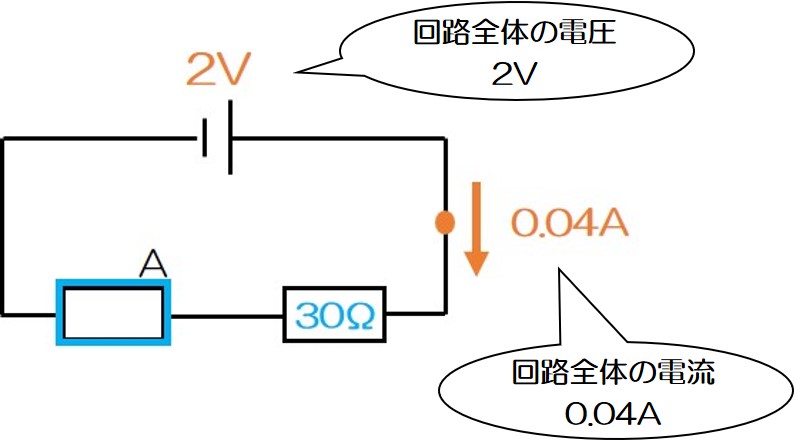
この2つがわかった時点で「回路全体の抵抗」を求めることができるね!
そう!「バオ~ムの式」で!
2 ÷ 0.04 = 50 50Ω
これで「回路全体の抵抗」が 50Ω だということがわかった!

さあ、ここで思い出そう!直列回路の抵抗の特徴について!

そう!つまり、さっきの↑の図の青枠に注目すると、
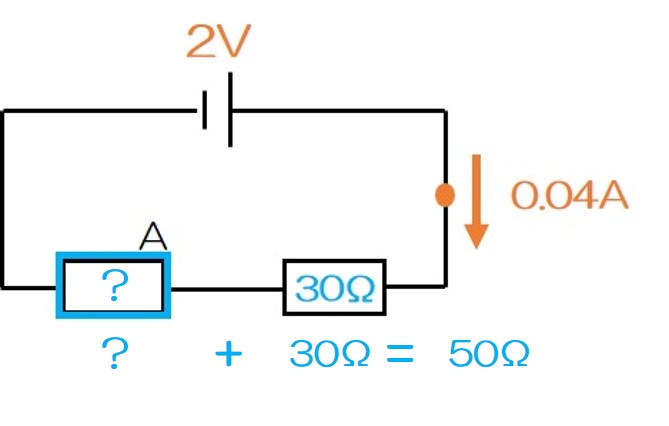
? + 30 = 50
の式が成立することになるのだ!
ここまでくるともう簡単だね~♪
抵抗器Aの抵抗は、
50 – 30 = 20 20Ω
図2の解説
まず注目すべきは「回路全体の電圧」と「回路全体の電流」!

この2つを使って「回路全体の抵抗」を求める!
そう!「バオ~ムの式」で!(しつこい笑)
ただし、計算するときは A (アンペア) でないとできないのでここで直してしまおう!
70mA = 0.07A

3.5 ÷ 0.07 = 50 50Ω
これで「回路全体の抵抗」が 50Ω だということがわかった!
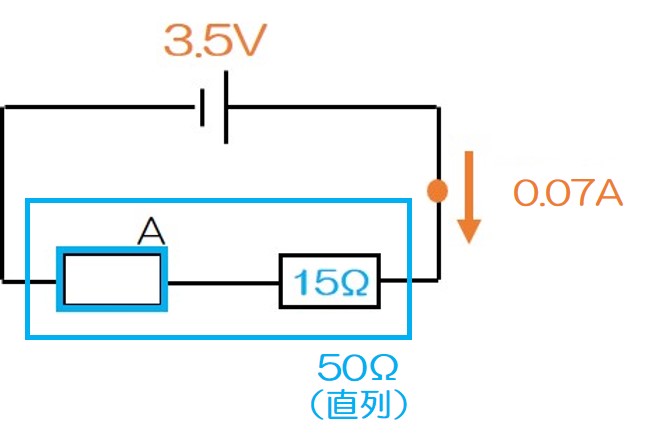
さあ、既に図1の問題をやったそこのキミ!直列回路の抵抗の特徴はもう完ぺきだろう!

そう!つまり、さっきの↑の図の青枠に注目すると、
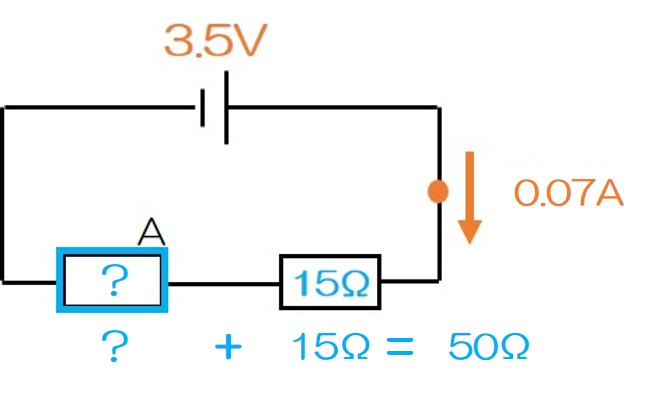
? + 15 = 50
の式が成立することになるのだ!
ここまでくるともう簡単だね~♪
抵抗器Aの抵抗は、
50 – 15 = 35 35Ω
図3の解説
この問題で注目すべきは「抵抗器Aに加わる電圧」と「抵抗器Aに流れる電流」!
まずは、「抵抗器Aに流れる電流」について見ていこう!
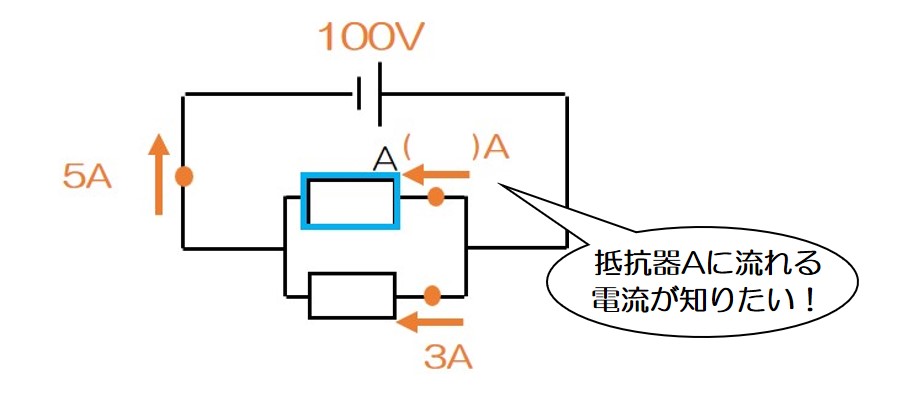
どうやって求めるかわかるかな~?
ヒントは「並列回路=電流の○○算」だよ!
思い出した?それならオッケー♪

そう!「並列回路=電流の足し算」だったよね!
というわけで、「抵抗器Aに流れる電流」は、
5 – 3 = 2 2A
次に、「抵抗器Aに加わる電圧」について見ていこう!
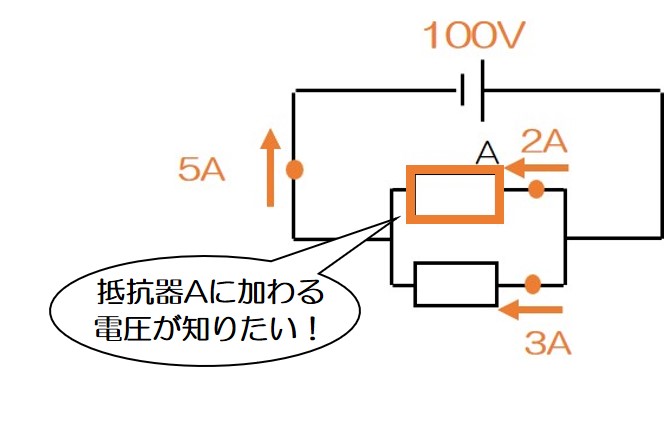
これはどうやって求めるかわかるかな~?
ヒントは「並列回路=電圧が○しい」だよ!
電圧が○しいの○に入る文字はどれかな?
1 恋 2 愛 3 等
1と2を選んだキミ!らいじんさんから10万ボルトをプレゼント♪

解説中に何やっとん!1億ボルトくらわしたろか~!
⚡⚡⚡ひゃ~!おへそだけは見逃して~!
(ひと休み)
それでは本題に戻そう!正解は3の「等」!
「並列回路=電圧が等しい」だね!
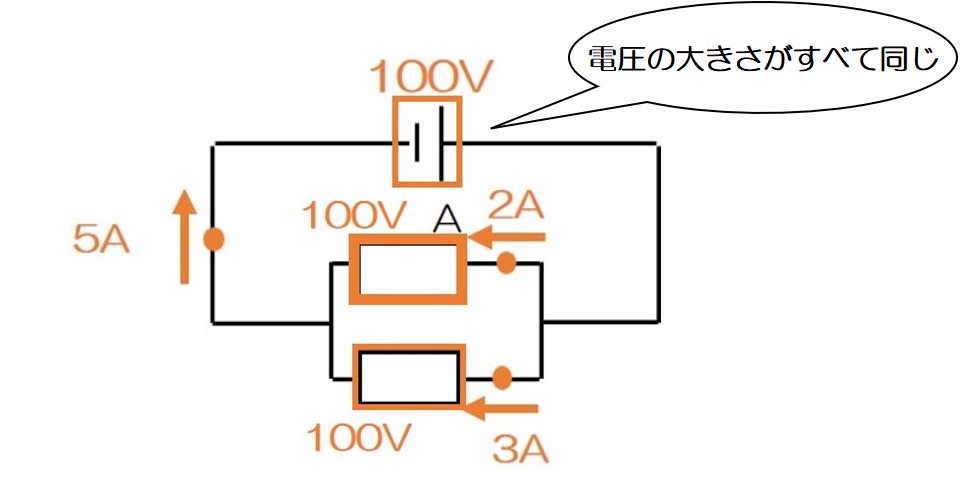
というわけで、「抵抗器Aに加わる電圧」は、100V
これで2つの要素が出そろった!

この2つを使って「抵抗器Aの抵抗」を求める!
そう!「バオ~ムの式」で!(あともう1回だけ言うよ笑)
よって、抵抗器Aの抵抗は、
100 ÷ 2 = 50 50Ω
図4の解説
この問題で注目すべきは「抵抗器Aに加わる電圧」と「抵抗器Aに流れる電流」!
まずは、「抵抗器Aに流れる電流」について見ていこう!

図3の問題が解けたなら大丈夫だよね!
ヒントは「並列回路=電流の○○算」だったね!
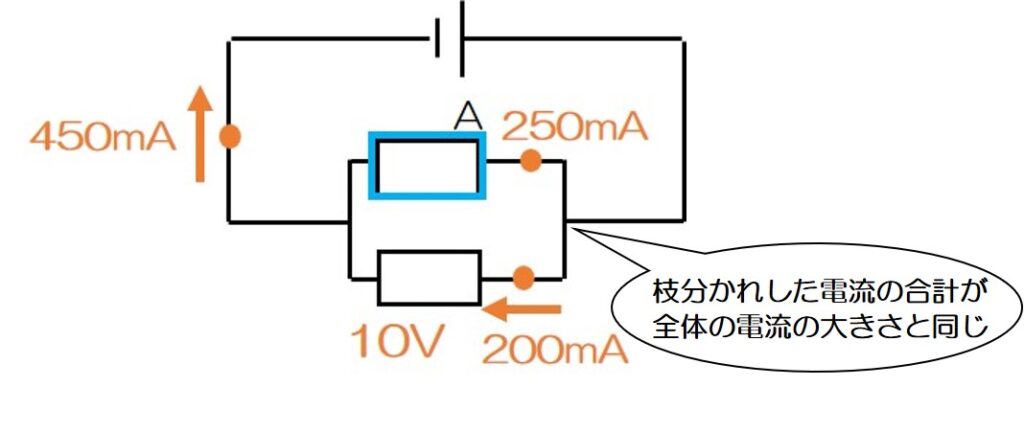
そう!「並列回路=電流の足し算」!
というわけで、「抵抗器Aに流れる電流」は、
450 – 200 = 250 250mA
ここで1つ大事なポイント!!
計算するときは A (アンペア) でないとできないんだったね!
250mA = 0.25A
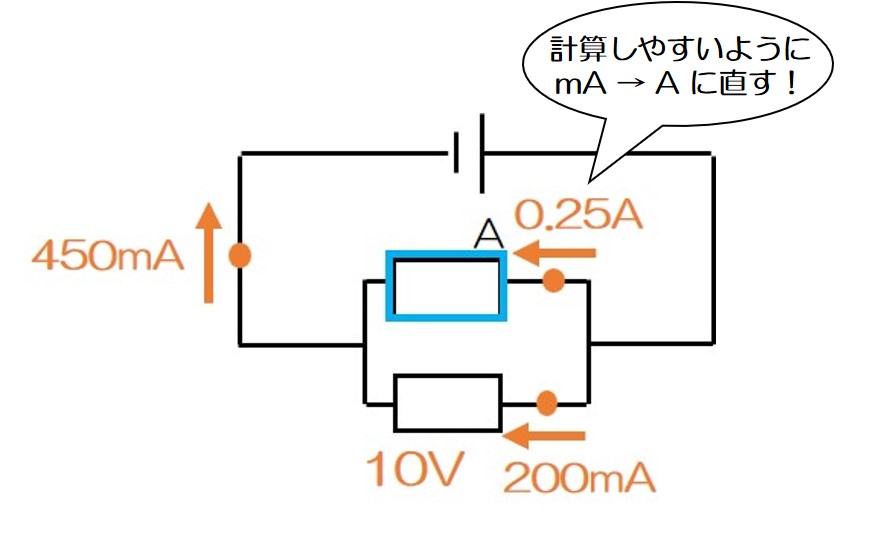
次に、「抵抗器Aに加わる電圧」について見ていこう!
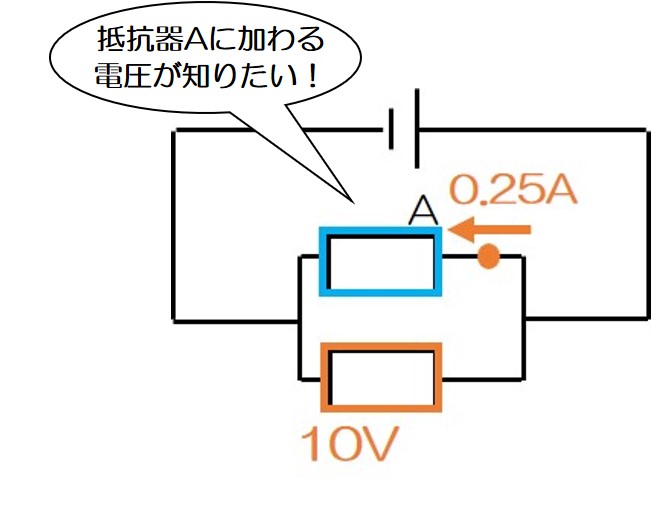
これももう大丈夫だよね?
ヒントは「並列回路=電圧が○しい」だったね!
今度はらいじんさんから1億ボルトをもらわないようにクイズは無しで…笑
そう!「並列回路=電圧が等しい」だね!
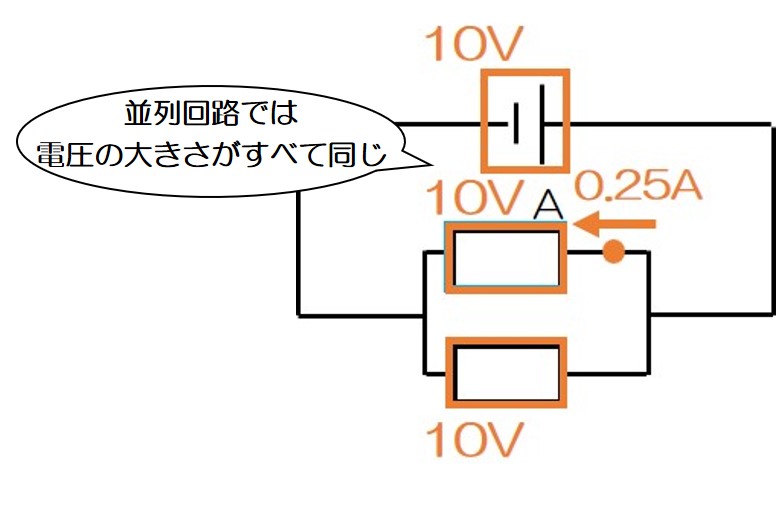
というわけで、「抵抗器Aに加わる電圧」は、10V
これで2つの要素が出そろった!
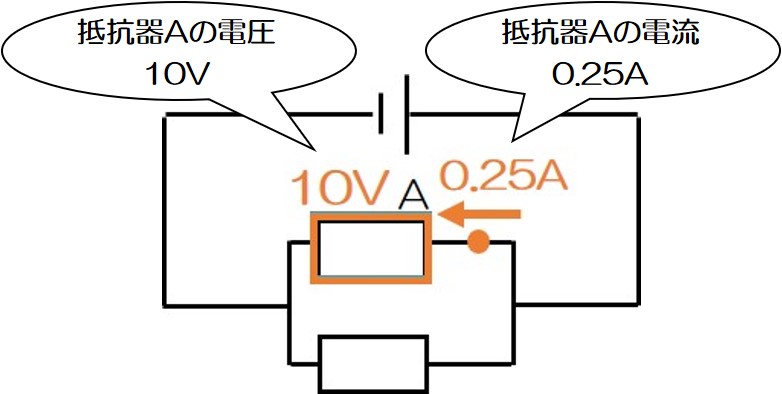
この2つを使って「抵抗器Aの抵抗」を求める!
そう!「バオ~ムの式」で!(こ・れ・で・さ・い・ご・だぁ~笑)
よって、抵抗器Aの抵抗は、
10 ÷ 0.25 = 40 40Ω

これでバオ~ムエキスパートや~♪


コメント