💡電流とは何だろう?

⚡ひゃ~!雷だ~!おへそを隠せ~!
雷って怖いけどカッコいいよね!君はどっち?笑
雷は、空気中を電流が流れる現象だね!
というわけで、今日はそんな電流についてやっていくよ!
それでは早速いってみよ~!

というわけで、今日は「電流」のお勉強や~!
ちなみに、らいじんさんは電流って何かわかるの?雷とのちがいは?ていうか雷鳴らせるの?雷鳴ると怖い?どうなの?

うるへ~!雷起こしたろか~!
⚡⚡⚡ひゃ~!すみません!おへそだけは~!
回路
💡まずは電流が流れる道筋について知ろう!
回路
電流が流れる道筋
◎回路の3要素
回路として成立するためには以下の3要素が必要である!
- 電流を流そうとするところ(電源)
- 電流が流れるところ(導線)
- 電気を利用するところ(負荷)

◎電流の向き
電流には向きがあり、電源の+極から-極に向かって流れる!
そのため、電流の向きが合わない電気器具は点灯しないこともある!
①豆電球の場合(電流の向きによらず点灯する)

②LEDの場合(決められた電流の向きでのみ点灯する)

◎回路の種類
回路はつなぎ方によって2種類に分けられる!
直列回路
1本の道筋でつながっている回路
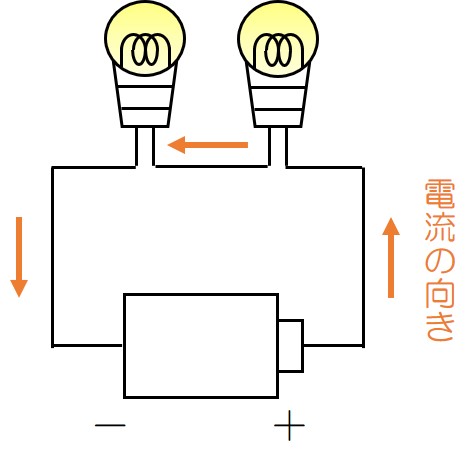
並列回路
枝分かれした道筋でつながっている回路
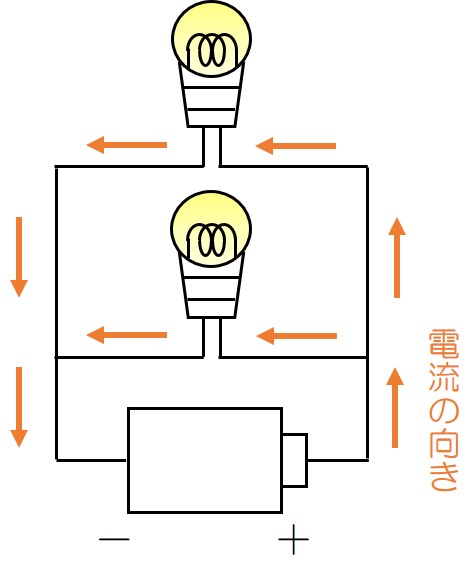
💡家庭用コンセントはどっちの回路かわかるかな?
正解は、並列回路!
1つの部屋の電気を消しても他の部屋の電気は消えないよね?
もし、自分の部屋の電気を消したときに家のすべての部屋の電気が消えたら…
あなたの家は直列回路です!笑

安心して暮らせるのは「並列回路」のおかげやで~!
回路図
💡次は回路の描き方について知ろう!
回路図
回路を電気用図記号で表したもの

◎回路図の5ルール
回路図をかくときは以下の5ルールを意識しよう!
- 電気器具は記号で
- 導線は直線で(定規を使って)
- 導線の曲がり角は直角で
- 導線の交わりは点で(T字はOK)
- 導線の角に器具はかかないで
それでは順番に見ていこう!
①電気器具は記号で
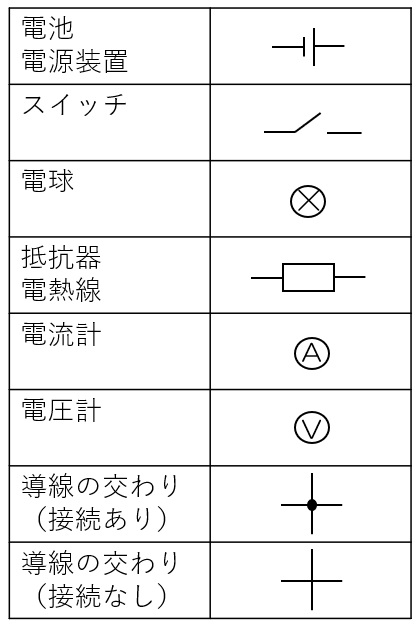
これらの記号は必ず覚えるようにしよう!
何回でもかいて練習だ~!
②導線は直線で(定規を使って)
③導線の曲がり角は直角で
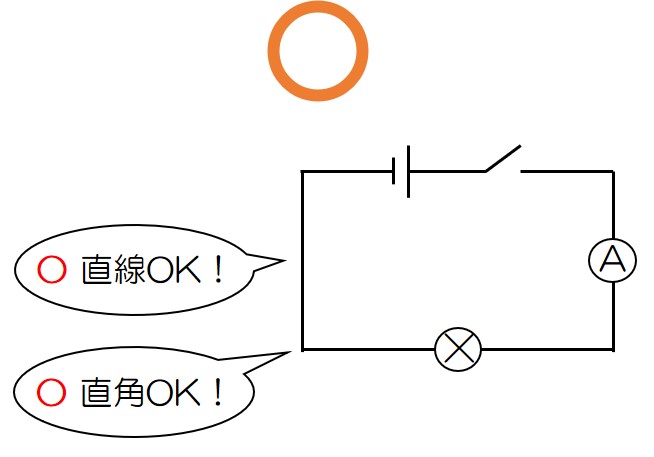
とにかく定規を使って、丁寧な直線や直角を意識しよう!
下にダメな例の、じゃがいも回路図を用意した!気をつけようね!

④導線の交わりは点で(T字はOK)

導線が交わっている部分には点を打っておこう!
ただし、↓のようなT字の部分は点を省略してもよいことになっている!
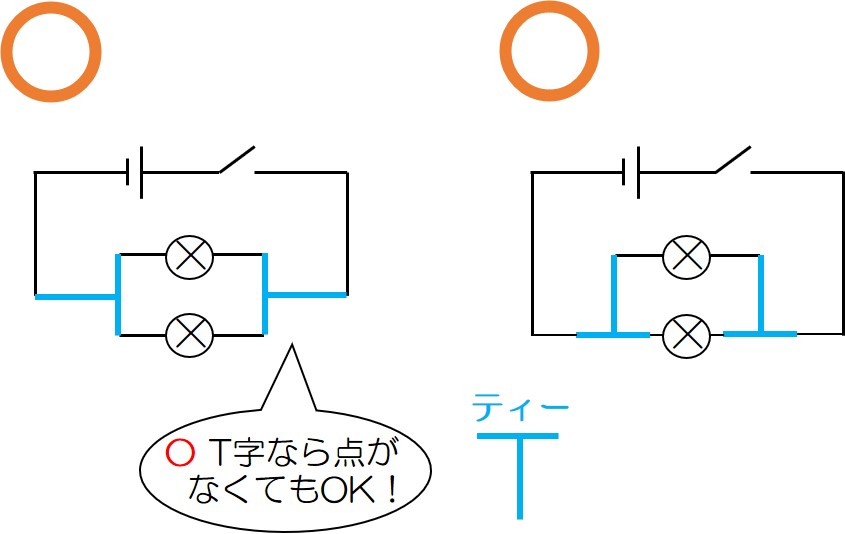
⑤導線の角に器具はかかないで

抵抗器の記号は覚えていたかな?回路が細かく枝分かれしているわけじゃないから注意してね!
下にダメな例の回路図を用意したよ!
なぜ角に器具をかくとダメなのかわかってもらえたかな?
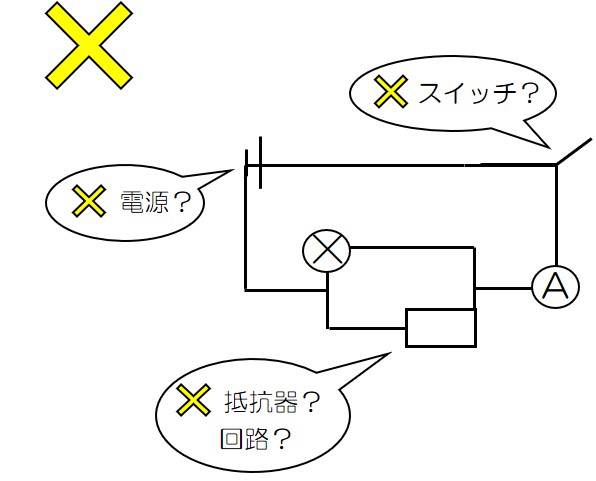

回路図は、図の美しさを意識するんやで♪
電流
まずは、電流の単位を紹介しよう!
【A】アンペア
【mA】ミリアンペア ☆1A=1000mA
次に、電流の大きさを測定する実験器具の紹介!
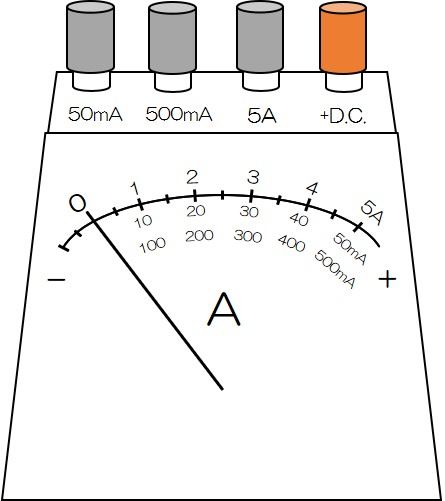
これは電流計と呼ばれる器具だよ!
回路に流れる電流の大きさを測定することができる優れもの!
それでは、電流計の使い方を見ていこう!
①電流を測定したい場所に直列につなぐ

直列とは、1本の道筋にすることだったよね!
もしも並列につなぐと、電流が流れすぎて電流計の針が振り切れちゃうので注意しよう!

②つないだ-端子は、針が目盛りいっぱいふれたときの値である
下の図を見てほしい!
針が同じ場所を指していても、つないでいる-端子の種類によって目盛りの読み方が変わるので気をつけよう!
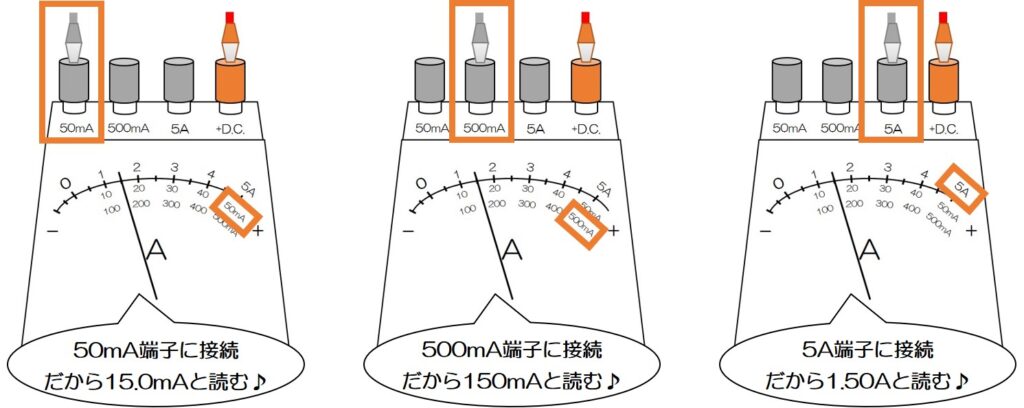
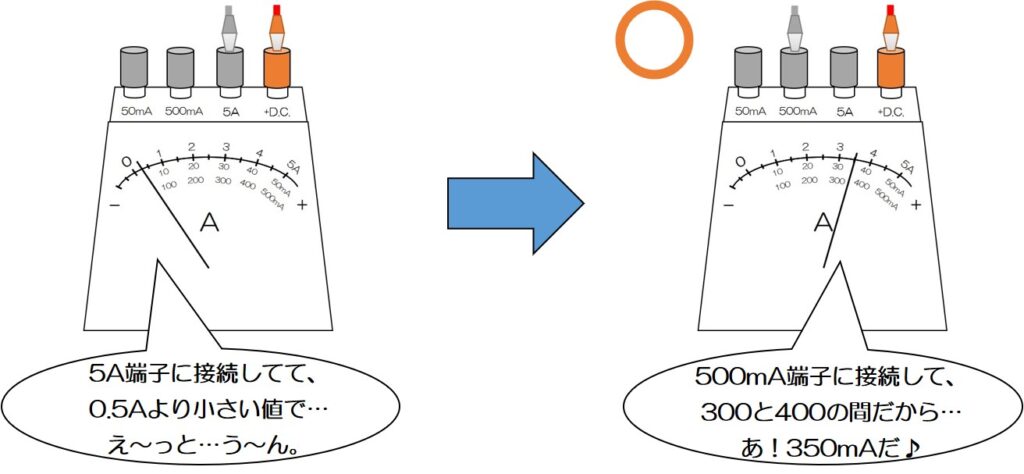
③5Aの-端子では測れない場合は500mAの-端子につなぎかえる
下の図のように、針の振れが小さくて読み取りにくいときは思い切って別の-端子につなぎかえよう!
◎直列回路に流れる電流
ここからは、電流を表す文字 I (Intensity of an electric current)を使って考えていくよ!
例:回路の中で、A点を流れる電流を IA とする
それでは、直列回路に流れる電流の特徴を見ていこう!

↑の図を見ると、この回路ではA~C点のどの部分で測定しても30mAの電流が流れているよね!
もちろん、2つの抵抗器にも同じく30mAの電流が流れている!
つまり、直列回路では流れる電流の大きさがすべて等しいということを覚えておこう!

シンプルに言うと、直列=電流が等しいや♪
◎並列回路に流れる電流
次に、並列回路に流れる電流の特徴について見ていこう!
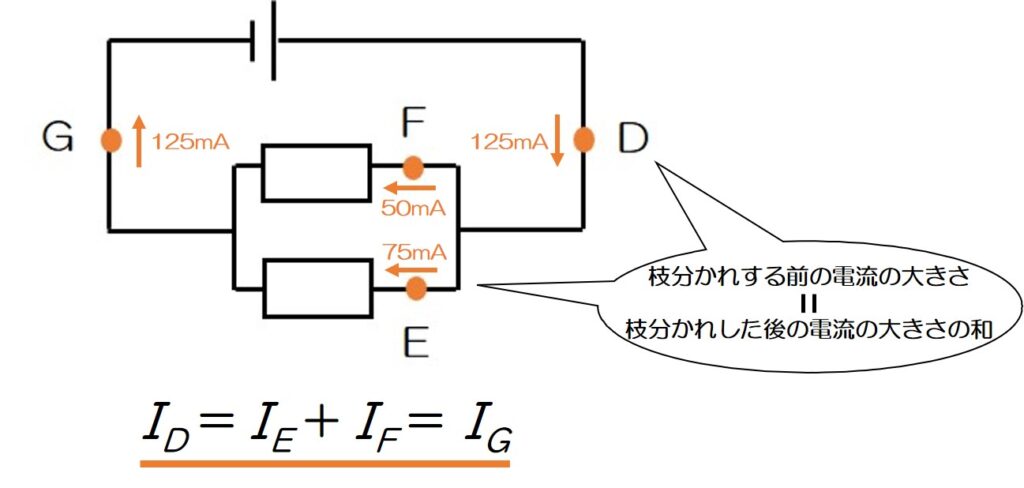
↑の図を見ると、この回路では回路全体としては125mAの電流が流れているね!(D点とG点)
並列回路は枝分かれしているので、全体の電流がEとFのそれぞれの枝に分配される!
そして、枝分かれした2つの電流を足すと元の電流の大きさにもどる仕組みになっている!
つまり、並列回路では枝分かれした電流の合計が元の電流の大きさと等しいということを覚えておこう!

シンプルに言うと、並列=電流の足し算や♪
電圧
電圧
回路に電流を流そうとするはたらき
まずは、電圧の単位を紹介しよう!
【V】ボルト
次に、電圧の大きさを測定する実験器具の紹介!

これは電圧計と呼ばれる器具だよ!
回路に加わる電圧の大きさを測定することができる優れもの!
それでは、電圧計の使い方を見ていこう!
①電圧を測定したい場所に並列につなぐ
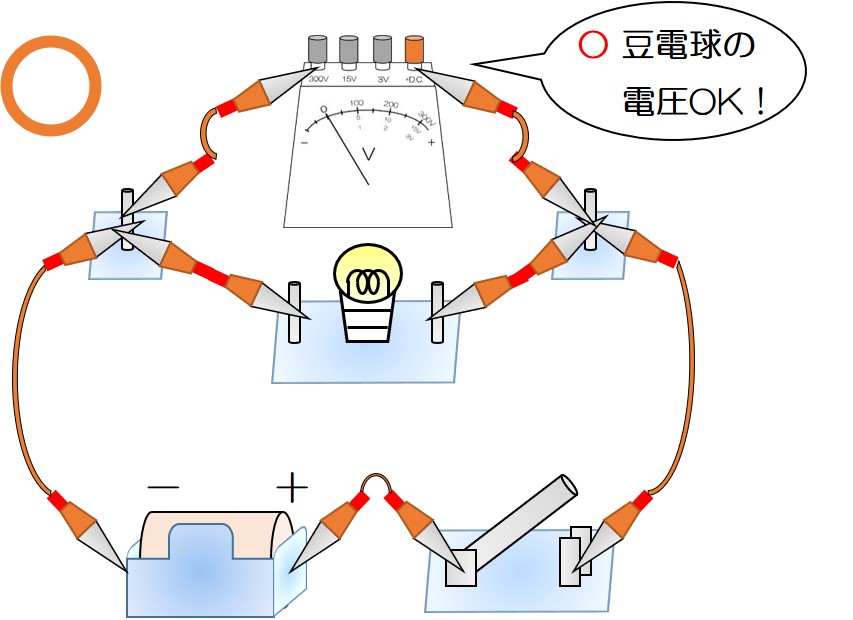
並列につなぐことで、「豆電球の電圧を測りたい」ということがわかる!
下の図のように、直列につなぐとどこの電圧を測りたいかがわからない!

※本当は、電圧計の中に抵抗があって、直列につなぐと回路に電流が流れにくくなることが問題
②つないだ-端子は、針が目盛りいっぱいふれたときの値である
先ほどの電流計のときと同様、針が同じ場所を指していても、つないでいる-端子の種類によって目盛りの読み方が変わるので気をつけよう!
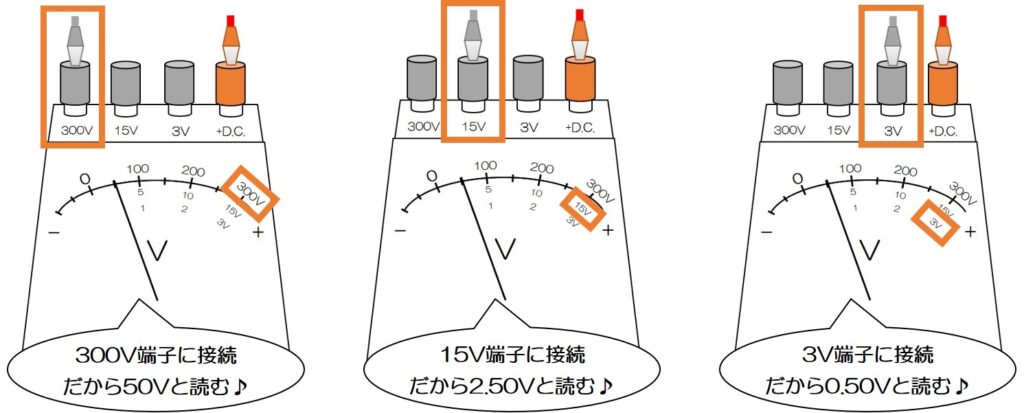
③300Vの-端子では測れない場合は15Vや3Vの-端子につなぎかえる
下の図のように、針の振れが小さくて読み取りにくいときは思い切って別の-端子につなぎかえよう!

◎直列回路に加わる電圧
ここからは、電圧を表す文字 V を使って考えていくよ!
例:回路の中で、A点を加わる電圧を VA とする
それでは、直列回路に加わる電圧の特徴を見ていこう!

↑の図を見ると、この回路ではA点とB点に加わる電圧を足し合わせると回路全体の電圧になっている!
つまり、直列回路では加わる電圧の合計が回路全体の電圧の大きさと等しいということを覚えておこう!

シンプルに言うと、直列=電圧の足し算や♪
◎並列回路に加わる電圧
次に、並列回路に加わる電圧の特徴について見ていこう!
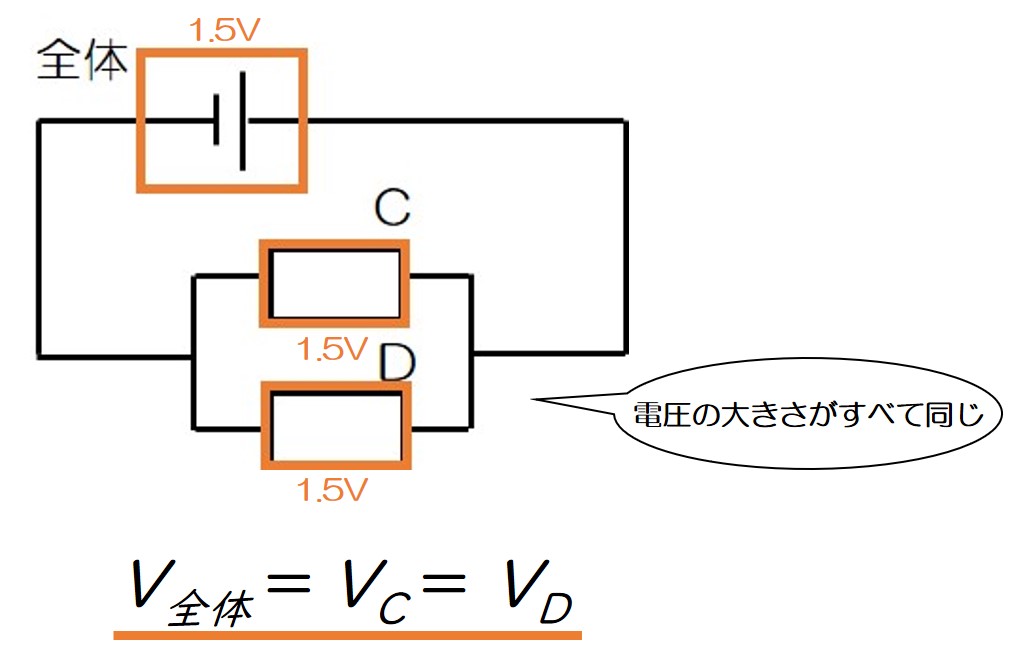
↑の図を見ると、この回路では回路全体に加わる電圧と、CとDのそれぞれの抵抗器に加わる電圧がすべて等しくなっている!
つまり、並列回路では加わる電圧の大きさがすべて等しいということを覚えておこう!

シンプルに言うと、並列=電圧が等しいや♪
抵抗(電気抵抗)
抵抗 (電気抵抗)
電流の流れにくさ
ここで、抵抗の単位を紹介しよう!
【Ω】オーム
それでは、抵抗とは具体的にどのようなものなのかを下の図で見てみよう!

並列回路なので、それぞれの抵抗器に同じ電圧がかかっている!
すると、抵抗の値が大きい30Ωの抵抗器には小さな電流が流れ
抵抗の値が小さい20Ωの抵抗器には大きな電流が流れている!
つまり、同じ大きさの電圧を加えたときに抵抗が大きい方が電流が流れにくくなることがわかる!

電流を流すことに抵抗するんやな♪
オームの法則
回路の中で、抵抗器に流れる電流の大きさは抵抗器に加わる電圧の大きさに比例する
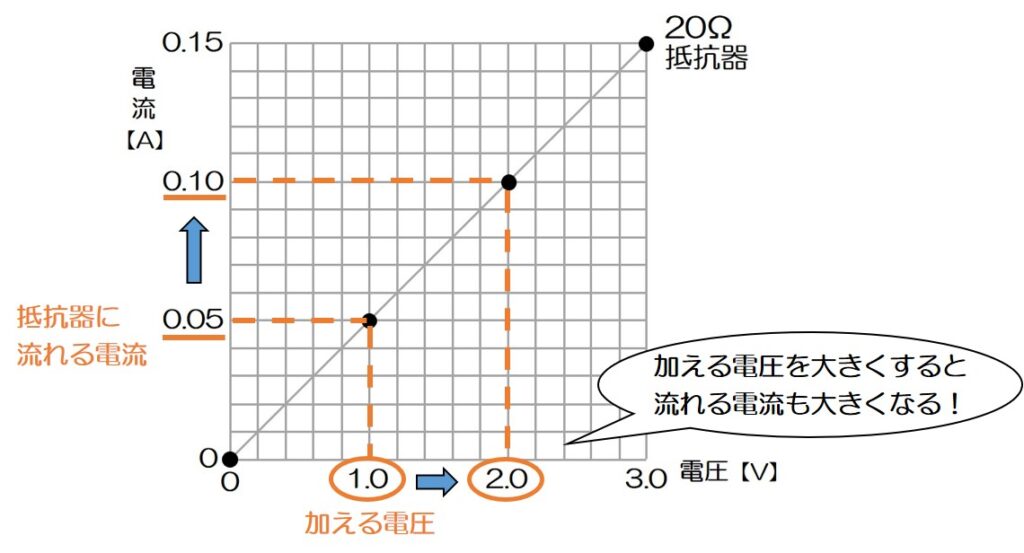
それでは、オームの法則を使って2本のグラフを読み取ってみよう!
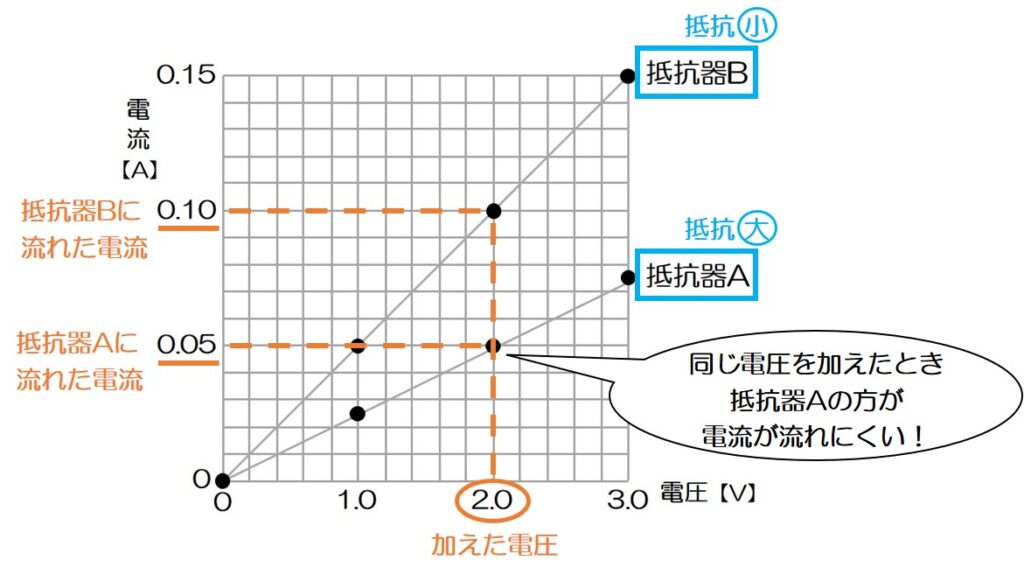
↑の図のように、2種類の抵抗器に同じ電圧を加えた場合、抵抗の大きい方には流れる電流が小さくなるよね!
つまり、グラフの傾きを見ればどちらの抵抗器の方が抵抗が大きいかが一目でわかる!
さらに、グラフの点が背景のマス目とぴったり重なっているところが見つかれば、具体的な数字で電流の大きさを表すことができる!
◎バオ~ムの式
数学で、「道のり÷時間=速さ」の式があるよね!
頭文字をとって「みはじ」っていうやつ!
「電圧」と「電流」と「抵抗」にも実はその関係が当てはまるんだ!
というわけで、それぞれの単位を表す記号を 「みはじ」っぽく並べちゃいました!
それがこの「バオ~ム」なのだ!

正確には、「ヴァオ~ム」だけどそこはいいよね笑
◎回路全体の抵抗
バオ~ムの式を使って「回路全体の抵抗」を求めていこう!
ここからは、抵抗を表す文字 R (Resistance)を使って考えていくよ!
例:直列回路全体の抵抗を R直 とする
それでは、直列回路を見てみよう!
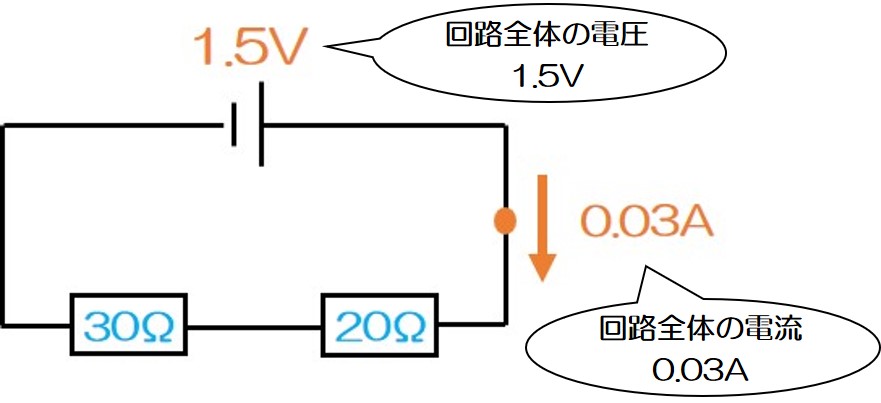
抵抗を求めるには、バオ~ムの式を使えばOK!
求めるための式は、「電圧÷電流=抵抗」だったね♪
直列回路の「全体の抵抗」を求めるには、「全体の電圧」と「全体の電流」がわかればいい!
○「全体の電圧」は電源の電圧そのまま(1.5V)
○「全体の電流」は直列回路なのでどこでも等しい(0.03A)
よって、これを計算すると
1.5 ÷ 0.03 = 50 50Ω
というわけで、計算で50Ωを求めることができましたぁ♪
ん?ちょっと待てよ……50Ω…。
20Ωと30Ωの抵抗を使って全体で50Ω……。
そうなんです、実は直列回路の全体抵抗はめちゃくちゃ簡単で↓
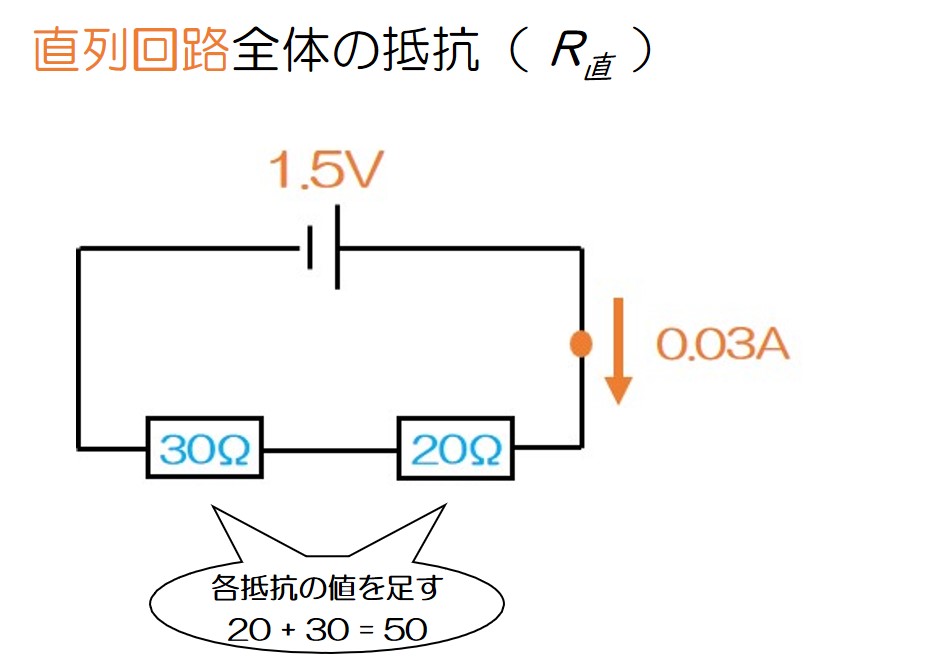
はい、それぞれを足せばいいだけなんです笑
つまりこれ↓

そんな特殊な公式あるんなら最初から教えてよ~♪バカちんが~♪って思うでしょ?
並列回路が難しいんだよね~😅
並列回路にも特殊な公式はある!
でも、そんなものに頼らず地道に計算して求めた方が絶対にいい!
それでは、並列回路をやってみよう!
並列回路全体の抵抗を R並 とする
並列回路の「全体の抵抗」を求めるには、「全体の電圧」と「全体の電流」がわかればいい!
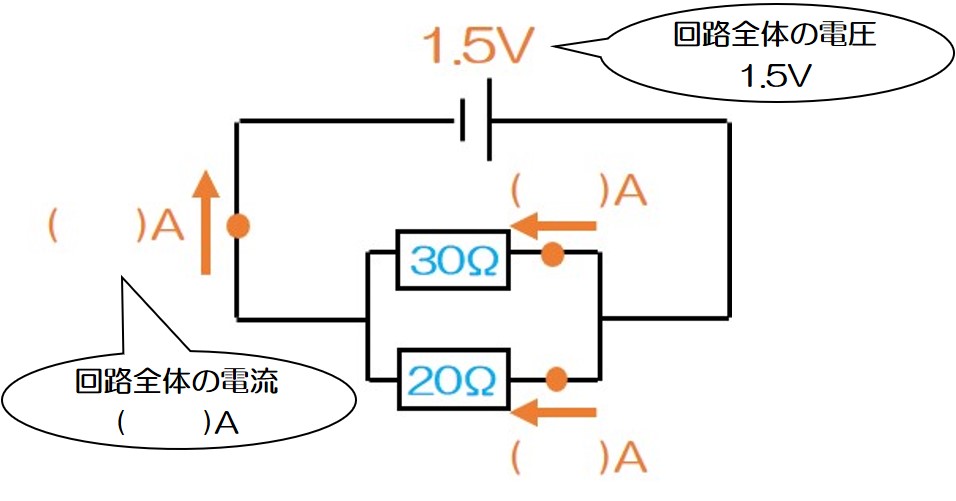
○「全体の電圧」は電源の電圧そのまま(1.5V)
○「全体の電流」はまだわからないね
というわけで並列回路で「全体の電流」 を求めるために、次の3ステップで考えていこう!
- 並列回路に加わる電圧の特徴を思い出そう
- 各抵抗に流れる電流を求めよう
- 回路全体の電流を求めよう
それでは順番に見ていこう!
①並列回路に加わる電圧の特徴を思い出そう
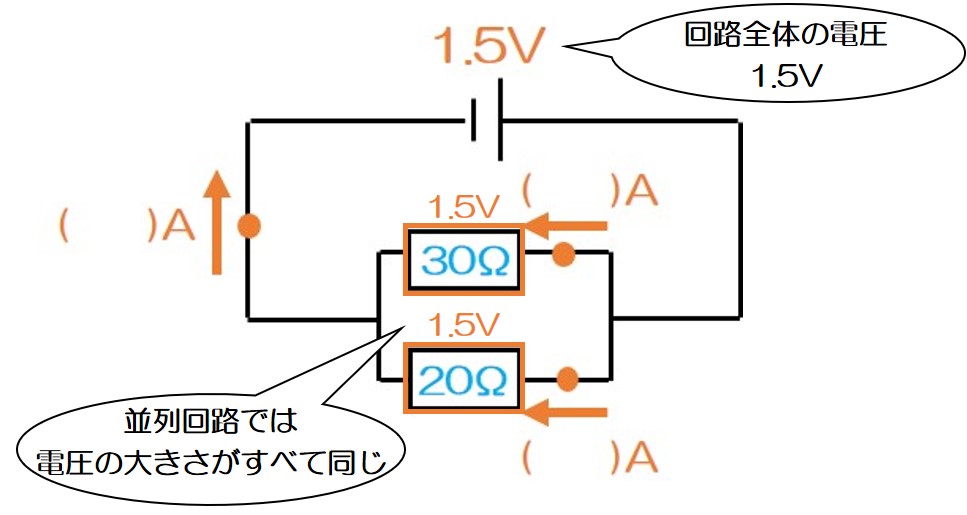
↑並列回路では加わる電圧の大きさがすべて等しいんだったね!
②各抵抗に流れる電流を求めよう
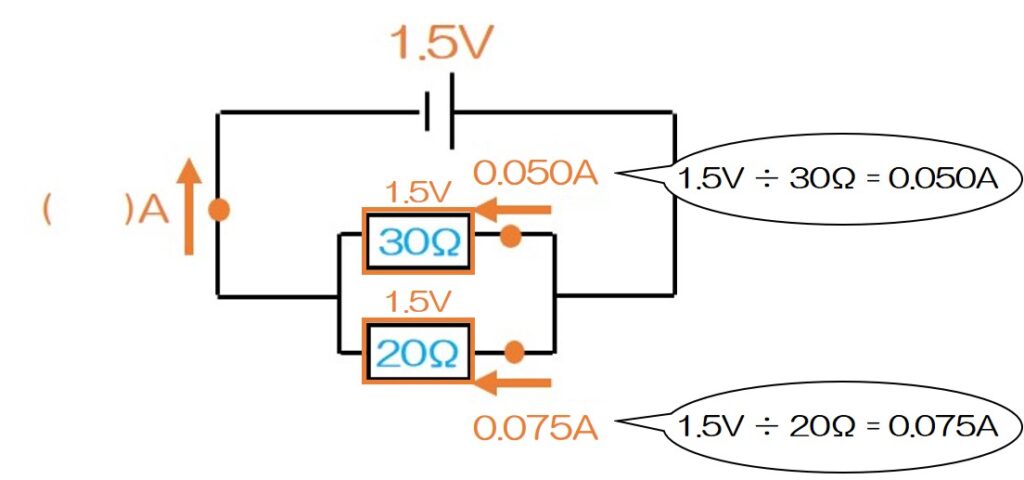
↑バオ~ムの式を使えばOK!
③回路全体の電流を求めよう
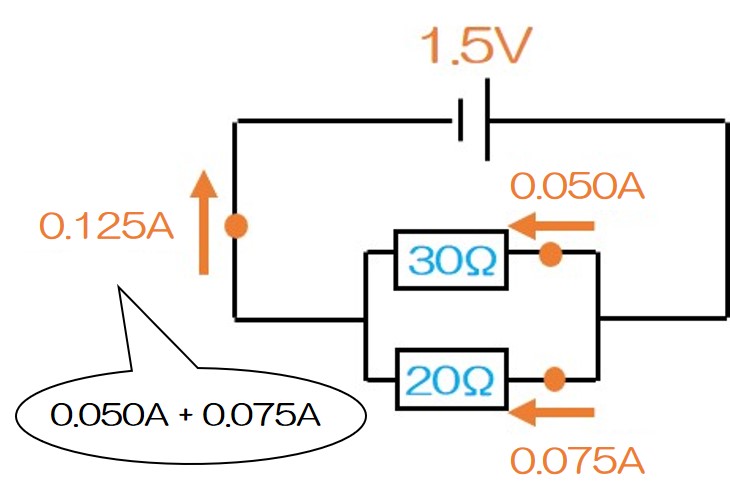
並列回路では枝分かれした電流の合計が元の電流の大きさと等しいんだったね!
これで「全体の電流」が出た!(0.125A)
よって、これを計算すると
1.5 ÷ 0.125 = 12 12Ω
というわけで、計算で12Ωを求めることができましたぁ♪
え?……12Ω…。
20Ωと30Ωの抵抗を使って全体で12Ω……。
小っっっさ!
そうなんです、実は並列回路の全体抵抗はめちゃくちゃ小さくなります!
それにしても20と30を使って12になる公式ってどんなんだ?
気になるね~💡
それでは、みなさんお待ちかねの公式を発表しよう!
見てビビらないでね!
どうぞ!

「・・・・・😅」
はい、公式は忘れましょう笑
実際に公式使わなくても計算で出せたし♪
でもどうしても気になる人!公式を使った具体的な計算は↓の図で見てね!

◎回路全体の抵抗と各抵抗の大きさの関係
それでは最後に!直列回路や並列回路の抵抗の大きさを一覧にまとめたものをご覧あれ!

↑のように、直列回路の全体の抵抗は最大に!
そして、並列回路の全体の抵抗は最小に!
これらのことをしっかりとおさえておきましょう!

抵抗の関係は R直 > RB > RA > R並 ってことやな♪
それでは、おつかれさまでした~♪


コメント